Tuottavuuden parannus ja mallit

Tuottavuuden parannus ja mallit (y= fx) + ε
Case: Sekoitekoe (mixture)

”Vaativin asia tuottavuuden parannuksessa on määrittää liiketoiminnan ongelma, jonka edessä olemme. Ihmiset kaikilla tasoilla pyrkivät välttämään tämän ja hyppäävät suoraan ratkaisuun, työkaluihin. Se mitä meidän tulee tietysti tehdä on suorittaa testejä/kokeita, mutta ennen tätä pitää saada paremmin rajattua ongelma, kohde, jonka tuottavuutta parannetaan.”

Dan Jones, Lean Enterprice Academy
Womak, Jones: The Machine that Changed the World 

Jos suunnittelet rakentavasi uuden omakotitalon, kesämökin, teetät vähänkään suuremman huoneistoremontin, tarvitset aina luvan ”ylemmältä taholta”. Luvan myöntämisen ehtona on jonkin asteiset suunnitelmat ja piirustukset, siis parempi ongelman rajaus.

Oletko ajatellut, miksi vaaditaan suunnitelma ja malli/piirustukset siitä, millainen ”parannusmuutos” tulee olemaan ja miten se vaikuttaa ympäristöön? Onko se vain ”ylemmän tahon” simputusta ja byrokratiaa vai olisiko sillä jokin tärkeämpi ja ylevämpi tavoite. Kuvaus positiivisesta ”ongelmasta”, rajaus parannuksesta laajassa mielessä!

Kun suunnitelma, talo, remontti, muutos on toteutettu, suoritetaan loppukatselmus ja hyväksytään tai vaaditaan lisäkorjauksia. Ja vielä tämäkin! – että pitäisi tehdä suunnitelma ja vielä noudattaakin sitä!

Ehkä tässä sitenkin on ”järkeä”! Olisiko sittenkin kysymys oppimisesta, testin/kokeen hyväksymisestä/hylkäämisestä ja johtopäätöksistä!

Onko yrityksen parannuksista ”piirustusta”?

Miten on yrityksessä? Tehdäänkö parannuskohteen valinta, suunnitelma ja malli? Kuinka parannus testataan? Kuinka testitulos analysoidaan? Hylätäänkö/ hyväksytetäänkö muutos ennen sen toteuttamista? Kuka päättää lopullisesta parannuksesta ja millä perusteilla?

Epäilenpä, että yrityksissä ei kovinkaan usein toimita näin. Niin usein törmään tilanteisiin, joissa hyvistä yrityksistä huolimatta ei ole saatu aikaan laatu- ja/tai tuottavuusparannusta mutta eipä ole suunnitelmiakaan, saati metodia.

Vain muutamissa isommissa yrityksissä on muodollinen muutos- /projektihallintamenetelmä lupa- ja katselmusmenettelyineen, mutta näissäkin yrityksissä harvoin parantamiseen liittyy ongelman valinta ja ”malli”-vaatimus, kausaalien yhteyksien kuvaus, myös numeerisessa muodossa. Syntyy syvä hiljaisuus, kun kysyy millä menetelmällä parannus toteutetaan.

Tunnetuin liikkeenjohdon numeerinen malli on varmaan DuPontin ROE/ROI -malli, joka kuvaa ongelman ja sitoo rahaprosessin kausaalitekijät ja antaa matemaattisen mallin^/1/. Tämän kaikkien pitäisi tuntea tai ainakin talousihmisten. Miten kirjanpito, tuloslaskelmat, analyysit tehtäisiin ilman malleja? Miten taloudellinen optimointi?

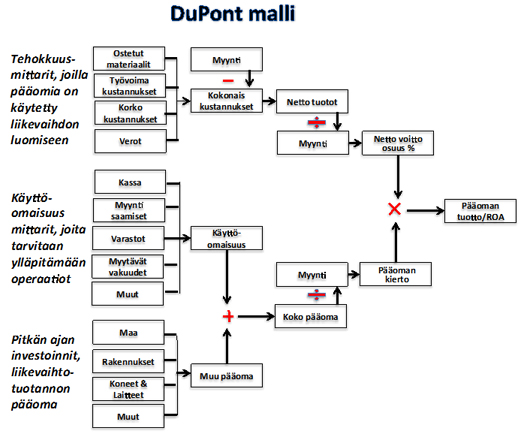
Ongelmalla (ROA/ROE/ROI/EBIT jne.) yhdessä talousmallien kanssa oli ja on ollut uskomattoman suuri merkitys yrityksille. Kuinka taloutta johdettaisiin ilman malleja?

DuPont -mallin ja yleensä kustannusmallien käytön ongelmana on, että ne esittävät kausaalimuuttujat kustannuksina (€). Parannus kuitenkin tapahtuu useimmiten ei-rahayksikössä vaan reaalimitoissa (m, kg, s jne.)

Leanin ”hukka, jaksoaika” tai Six Sigman ”hajonta, sigma” eivät esiinny valitettavasti DuPont- ja kustannuskaaviossa. Niitä ei ole suoraan sidottu yrityksen rahaprosessin tavoitteisiin ja malleihin, vielä!

Operaatiotiede, tehdasfysiikka, Factory Physics^/1/, tarjoaa yhdyssiteen reaaliprosessin ja rahaprosessin välille. Johdettu malli sitoo operaatiot rahaprosessiin ja samalla paljastuu jaksoajan (Lean) ja vaihtelun (Six Sigma) vaikutuskanavat – kausaliteetit. Kuva 2

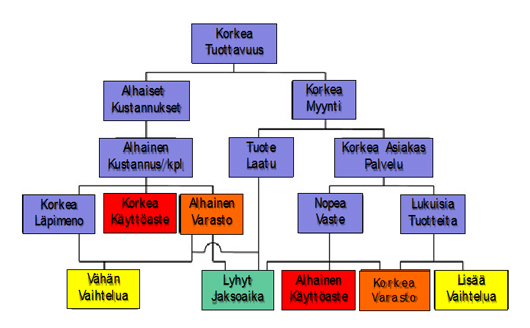
Tämäkään malli ei anna yksiselitteistä ohjetta, mikä on ongelma, mitä pitäisi parantaa – kun teet parannuksen yhteen ”pyllistät” toiselle (korkea käyttöaste <=> alhainen käyttöaste, korkea varasto <=> alhainen varasto jne.). On siis luotava optimointimalli, joka huomioi tekijät ja niiden vaikutukset ja etsii ”yhteisen” hyvän eli optimin. Parannus vaatii optimoinnin – tuoton ja panosten välisen kompromissin! Optimointi vaatii aina kvantitatiivisen lähestymistavan, yhtälön.

Lean Six Sigmassa raha- ja reaaliprosessin välinen yhteys ”luodaan” huolellisella projektin valinnalla yhdistettynä tuottolaskelmaan, jonka yritysjohto/Champion hyväksyy. Hän myös hyväksyy projektin päätyttyä toteennäytetyn parannusehdotuksen.

Tämä on syy, miksi Lean ja Six Sigma -koulutuksiimme on sisällytetty erillinen Champion -koulutus.

Ongelma ja mallivaatimus on Lean Six Sigmassa ehdoton – DMAIC – ja lisäksi itse parannus on esitettävä kausaalissa funktiomuodossa y= f(x) + ε.

Tämä selittänee, miksi Lean Six Sigma -projektit onnistuvat n. 20-25 kertaa todennäköisemmin kuin ”tavanomaiset” listaparannukset^/2,3/.

Parannusmalli ja ”tavanomainen” malli

Parannuksessa käytettävä malli ja vaikkapa rakennuspiirustus tai ”ruokaresepti”, joka sekin on malli, poikkeavat toisistaan siinä, että rakennuspiirustus tai resepti esittää tunnetun ratkaisun, kun taas parannuksessa konkreettista ratkaisua ei ole tiedossa.

On mielenkiintoista, että jopa siinäkin tapauksessa, jossa ”tiedämme” konkreettisen ongelman ja ratkaisun, mallin (piirustuksen) tekeminen ennen toteuttamista on suositeltavaa ja osin pakollista. Japanilaiset kutsuvat tätä A3 tai QC-story:ksi. Muutoksen toteuttaminen on riskialtis! Lotossa ongelma on voittaa rahaa ja ratkaisu on ”oikeat numerot, 4-7 kpl”, vaan kun ei ole metodia, menetelmää valita oikeuta numeroita!

Parannuksessa (improvement) ratkaisua ei ole tiedossa, joten riski epäonnistua on erittäin suuri (n. 95-98 %). Tällöin on tärkeää noudattaa tutkittua ja hyväksi havaittua reittiä. Walter A. Shewhart^/4/ ja myöhemmin W. Edwards Deming^/5/ esittivät ensimmäisen parannusreitin, PDSA-ympyrän. (testiympyrä, johtamisympyrä). Myöhemmin tästä reitistä, polusta, on muotoiltu yksityiskohtaisempia kuvauksia – PDSA muotoutui DMAIC-prosessiksi. Kuva 3.

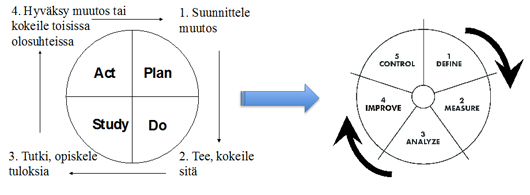
Näitä reittejä kutsutaan roadmapeiksi (kuva 4) tai protokolleiksi, joilla hallinnoidaan yksittäisten työkalujen ja analyysien joukkoja.

Mitä vaativampi on työ, sitä huolellisemmin on noudatettava ylätason menettelyjä. Yleensä myös analyysityökalujen määrä ja laatu lisääntyvät. Kysymys on onnistumisesta. Etukäteen suunniteltu tai valittu reitti lisää merkittävästi onnistumista 2-5 % -> 65-85%:iin.

Katso kokemuksia Lean Six Sigmasta (esimerkkejä ja kuvauksia projekteista) www.sixsigma.fi.

Lean Six Sigma ja yhtälö y= f(x) + ε

Lean Six Sigmassa mallinnus viedään tätä ylätason protokollamallia pidemmälle aina ”yksityiskohtaisen rakennuspiirustuksen” tasolle – kausaaliin syy-seuraus malliin, jolla voidaan tulos ennustaa ja optimoida. Malli on luotavissa vain kokeellisesti (DoE, Taguchi) eli tieteellisesti. Ennen lopullista parannuksen toteuttamista malli vielä osoitetaan oikeaksi eli konfirmoidaan ja verifioidaan.

Mallin laatiminen onnistuu kaikkien mitattavissa tai arvioitavissa olevien tuote tai prosessiominaisuuksien suhteen. Minitab muodostaa ”automaattisesti” mallin y= f(x) + ε, kun mallin muuttujat x on määritetty ja ulostulodatoja y on kerätty rationaalisesti, suunniteltu koe/testi (DoE -matriisin mukaisesti, jotka on luetteloitu ohjelmassa).

Malli mahdollistaa parannuksen, optimoi ja ennustaa tulevan ja antaa virheen ε. Systeemin parannukseen tarvitaan yleensä 4-6 tekijän yhtäaikainen optimointi. Toisin sanoen useat tekijät ovat ulostulon suhteen keskenään ristiriidassa ja on löydettävä optimi, yhteinen ”hyvä”. Minitabilla voidaan optimoida 2-49 tekijää samanaikaisesti ja jopa 25 eri ulostuloyhdistelmälle. Tämä vaihe edustaa DMAIC -prosessissa parannusvaihetta I (Improve).

Case: Kotitekoinen ikkunanpesuaine. Sekoite eli Mixture DoE

Teollisuudessa eräs keskeisiä ongelmia on kemiallisen reseptin optimointi (esim. paperin pinnoitteet, liimat, maalit, hartsit, polttoaineet, räjähteet jne.)

Tarkastellaan ongelmaa yksinkertaisen kemiallisen sekoitteen (Mixture) avulla, jolla optimoidaan 3 sekoitekomponenttia, 1 prosessikomponentti ja 2 ulostulokomponenttia.

Tarkoituksena on valmistaa ”kotitekoinen” ja edullinen ikkunanpesuaine, jonka pH on 8 -10 ja aine olisi halvempaa kuin kaupan ikkunapesuaine. Prosessi etenee PDSA-jaksona. PDSA-kuvaan 5 on täydennetty ”laajennettu” koesuunnitteluprotokolla.

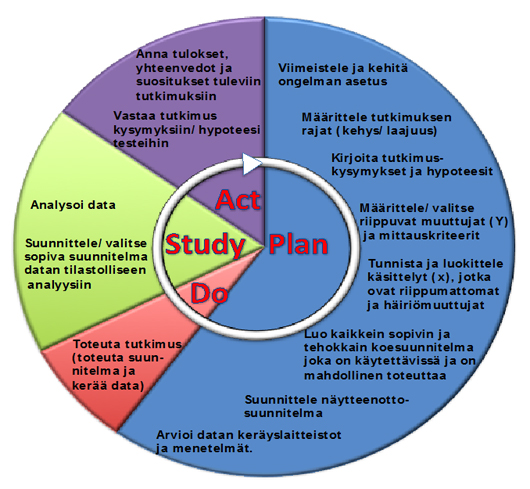
Resepti: Vanha äidin ohje oli, että kun ikkunapesuveteen lisää astianpesuainetta ja lorauksen etikkaa ikkunat tulevat kirkkaiksi, mutta valitettavasti pH putoaa silloin 3-4 paikkeille. Mäntynestesaippuaa lisäämällä pH:n voisi saada halutulle tasolle. (Huom. Esimerkissä ei talvesta johtuen testata pesutulosta. Onnistuisi helposti arviointiasteikolla 1-10 .)

Koevälineinä käytetään:

Komponentit:

• Astianpesuaine, mäntynestesaippua, väkiviinaetikka, vesi
• pH-liuskoja
• Mittasarja
• Muovimukeja

Kustannustiedot: Astianpesuaine 1,85 €/l, Mäntynestesaippua 1,69 €/l, Väkiviinaetikka 1,32 €/l, Muovimuki 0,016 €/kpl, Mittaliuska 0,32 €/kpl. (Ikkunanpesuaine 2,98 €/l)

Suunnittele, Plan

Mallin y= f(x)+ε luominen tapahtuu keräämällä koedataa tietyllä tavalla. Käytetään Minitab Mixture -koesuunnitelmaa Simplex Centroid -koesuunnitelmaa. Valitaan 3 tekijää ja 1 prosessimuuttuja (vesi).

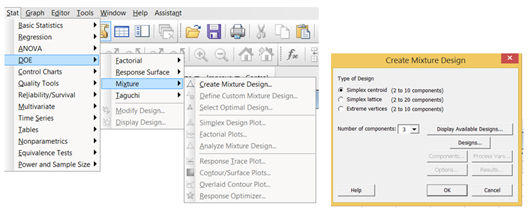
Tee, Do

Luodaan koesuunnitelma ja tehdään sekoitteet (mixture) mukeihin, mitataan liuskoilla pH-arvot ja määritetään jokaiselle koepisteelle koenesteen kustannus + välinekustannus (muki + liuska). Kustannukset saadaan laskemalla jokaiselle yhdistelmälle kustannus.

Tuloksena saadaan seuraava Minitab data. X-muuttujia (kausaali) ovat Astianpesu, Mänty, Etikka ja prosessimuuttuja Vesi ja ulostulot Y pH ja Kustannus/litra.

Tutki, Study

Datasta Minitab muodostaa automaattisesti Six Sigma -yhtälön y= f(x)+ε molemmille ulostulomuuttujille.

Analyysistä voidaan lukea yhtälöt pH:lle ja Kustannus/litra

pH:n yhtälö:

Y_pH= 0,97*Astianpesu + 2,11*Mänty +0,43*Etikka – 0,12*Astianpesu*Mänty + 0,14*Astianpesu*Etikka – 0,33*Mänty*Etikka ± 0,57

Kustannus/litra -yhtälö:

Y_kustannus/l= 0,38*Astianpesu +0,35*Mänty +0,27*Etikka ± 0

Optimointi

Minitab optimoi asetetut arvot ja hakee lukuisten ratkaisujen joukosta yhden tai useampia ratkaisuja Optimizer -funktiolla. Tässä pH arvoa on painotettu Weight = 10 ja myös tärkeys Importance = 10.

Huomaa, että eri tekijät ovat keskenään ristiriidassa. Kun toinen kasvaa niin toinen pienenee. On löydettävä yhteinen ”hyvä”. Ratkaisuja on lukuisia. Yksi löydetty Optimi on Astianpesuainetta 1,11 Mänty 3,2 Etikka 0,60 ja vesi 7,5. (punaiset arvot). Näillä arvoilla saadaan pH 8,0075 ja Kustannus/l= 1,7499 €/l.

Vielä on määritettävä luottamusrajat arvoille. pH arvon keskiarvo on 95% luottamuksella välissä ε =7,54 – 8,46 ja yksittäinen sekoite ε = 6,69 – 9,31.

Seuraavaksi tehdään sekoitteella konfirmaatio. Tehdään saadulla reseptillä muutama sekoite ja mitataan, onko kyseinen sekoite laskettujen rajojen sisällä. Tässä näin oli pH = 8,02.

Toimi, Act

Löydettiin sekoite, joka täyttää vaatimukset ja malli konfirmoituu. Testattu resepti on 1,23 €/litra halvempaa, kuin valmis ikkunanpesuaine. Nyt olemme valmiit esittelemään ratkaisun yritysjohdolle.

Yhteenveto

Ongelman nimeäminen, asettaminen riittävän konkreettiseksi on yksi keskeisistä tuottavuuden parannusedellytyksistä. Ei riitä yleisesti vain hukan, hävikin, kustannusten vähentäminen. On löydettävä optimi tekijöiden välillä. Meillä edelleen vallitsee energian ja aineen häviämättömyyden laki. Hukkaa ja vaihtelua ei voi poistaa, mutta sen voi muuttaa toiseen ”muotoon” eli optimoida, jota sitten eri nimellä kutsutaan!

On myös oltava etukäteen nimetty suunnitelma tai menetelmä jota noudatetaan joko tunnetun ratkaisun toteuttamisessa tai tuntemattoman ratkaisun etsimisessä. Muuten ollaan Lotossa – toivotaan miljoonaa, tunnetaan numerot, mutta ei numeroiden valintamenetelmää! Tunnetuin parannusmenetelmistä on koe-/testiympyrä PDSA.

Muutoksen varmistamiseksi on parannusehdotus testattava ja mahdollisesti optimoitava lukuisten keskenään ristiriitaisten ominaisuuksien ja tulosten suhteen. Tämä vaatii kvantitatiivisen ennusteyhtälön, mallin, luomista.

Nämä kaikki toteutuvat Lean Six Sigma DMAIC -parannusprojektissa ja VSM (Lean) -projekteissa.

Katso video mixturekokeesta (Case: omatekoinen ikkunanpesuaine):

Lähteet:

1. Edwards Pound, Jeffery Bell, Mark Spearman; Factory Physics for Managers – How Leaders Improve Performance in a Post-Lean Six Sigma World, 2014
2. S.S. Chakravorty: ”Where Process-Improvement Projects Go Wrong.” Wall Street Journal, June 14, 2012
3. J.M. Juran: Quality Handbook, Sixth edition, 2010
4. Walter A. Shewhart; Economic Control Of Quality of Manufactured Products, 1931
5. W. Edwards Deming: Out of the Crisis, 1983
6. John Cornell: Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data, 2002