Parannusprojektien hallinta ja Monte Carlo

Minitab Inc:n parannusprojektien hallintaan ja toteutukseen tarkoitettu Minitab Engage (entiseltä nimeltään Companion) on sisältää joukon valmiita etenemismalleja erityyppisille metodeille, sekä kattavan valikoiman työkaluja projektien eri vaiheisiin. Lukuisten työkalujen lisäksi Engage ja myös sitä kevyempi Minitab Workspace sisältävät Monte Carlo-simuloinnin.

Minitab Engage -ohjelmalla pystytään hallitsemaan, seuraamaan ja jakamaan oleellista tietoa projektien etenemisestä, nykyisestä tilasta ja saavutetuista hyödyistä. Ohjelman tarkoituksena on siis helpottaa projektien hallintaa ja tehdä laadun ja prosessien parantamisesta läpinäkyvämpää. Siinä missä Minitab tilasto-ohjelmisto on työkalu datan graafiseen ja tilastolliseen tulkintaan, on Engage väline projektien toteuttamiseen, hallintaan ja johtamiseen. Engage mahdollistaa projektien etenemisen seuraamisen ja niiden koordinointia voi seurata modernin pilvipalvelun kautta, jolloin kaikilla projektien ja prosessien avainosakkailla on pääsy oleelliseen ja reaaliaikaiseen tietoon. Minitab Workspace on Engage ohjelmiston kevyempi versio ja sisältää muut toiminnollisuudet, lukuun ottamatta projektien seurantaa ja hallintaa pilvipalvelun kautta.

Ohjelmasta löytyy valmiit etenemismallit tai pohjat erilaisille prosessien kehittämisen menetelmille, kuten esim. Lean Six Sigman DMAIC, DFSS tai Lean Kaizen tapahtumat. Myös organisaation omien menetelmäpohjien luominen on täysin mahdollista. Työkalujen joukko sisältää sopivia työkaluja jokaisen menetelmän eri vaiheisiin, kuten mm. CT-puu, SIPOC, arvovirtakuvaus VSM, prosessikartat, FMEA, sekä tietenkin kaikki tarvittavat kaavake-ja dokumentaatiopohjat. Valmiissa projektipohjissa on toimintaa ohjaava ominaisuus, joka on varmasti hyvä standardoimaan organisaation sisäisiä toimintatapoja.

Monte Carlo -simulaatio

Yksi mielenkiintoisimmista työkaluista Engage ja Workspace -ohjemissa on Monte Carlo-simulaatio. Alun perin atomipommin kehitystyön sivutuotteena syntynyt Monte Carlo-simulointi on menetelmä, jolla pystytään simuloimaan prosessin kyvykkyyttä prosessin ulostuloa kuvaavan mallin avulla. Rakennettavan mallin osaset perustuvat joko tiedettyyn käyttäytymismalliin tai on luotu koesuunnittelun (DoE) tai regressioanalyysin avulla.

Malli siis esittää, kuinka prosessin tekijät (x1…xn) vaikuttavat prosessin ulostuloon Y. Mallin tekijöille määritellään jakauman tyyppi ja sen arvot, kuten keskiarvo ja standardipoikkeama. Nämä tekijät perustuvat joko mittausdataan tai arvioituun tilanteeseen.

Tekijöihin siis liitetään riski ja epävarmuus niiden toteutumisesta. Kun prosessia simuloidaan esimerkiksi 50 000 kertaa, saamme arvion mallin mukaisen prosessin ulostulon Y:n käyttäymisestä. Mallinnusta ja simulointia voidaan käyttää esimerkiksi uusien valmistus -tai palveluprossien kyvykkyyden arvioinnissa tai suunnittelussa. Tämä on usein huomattavasti turvallisempaa ja halvempaa, kuin vastaavat kokeilut reaalisysteemillä.

Ensimmäisen simulaatioajon jälkeen ohjelma antaa meille työkaluja mallin parantamisen tutkimiseen. Työkaluja on kaksi, optimointi ja herkkyysanalyysi. Optimointityökalulla voidaan määrittää uudet arvot, joiden väliltä mallin tekijöitä lähdetään hakemaan, jotta saataisiin parempi lopputulos. Voimme asettaa halutuksi optimiksi tietenkin niin ulostulo(je)n maksimoinnin, minimoinnin, tietyn tavoitteen tai virheellisten kappaleiden minimoinnin. Vastaavasti herkkyysanalyysillä voidaan selventää, minkä muuttujan hajontaa muuttamalla prosessimme kyvykkyys paranee eniten. Eli minkä tekijän vaihtelun pienentämisestä saamme parhaan vaikutuksen ulostulossa.

Hankintaprosessin simulointi Monte Carlo -menetelmällä

Voisimme esimerkiksi simuloida hankinta- tai ostoprosessin jaksoaikaa hankintapäätöksen tekemisetä tavaran toimittamiseen Monte Carlo-simulaation ja yksinkertaisen mallin avulla, jossa ostoprosessin aika = tarjouksen määrittäminen + vastaukset + päätös + toimitus kuluneina vuorokausina. Mallin muuttujissa on mahdollista käyttää erilaisia todennäköisyysjakaumia, tai datan avulla valita muuttujan käyttäytymistä kuvaava ja mallintava jakauma.

Tässä tapauksessa tarjouksen määrittämiseen ja luomiseen käytettyä aikaa kuvaa tasajakauma, jossa 2-4 päivää ovat kaikki yhtä todennäköisiä. Vastausten odottamista ja päätöksentekoa taas kuvaavat kolmiojakaumat, joissa on arvioitu pahin, keskimääräinen ja pahin tapaus (kuten projektinhallinnan PERTT-menetelmässä). Vastaavasti toimitusaikaa kuvaa meillä normaalijakauma, jonka keskiarvo on 21 päivää ja standardipoikkeama 4 vuorokautta. Tässä tapauksessa enimmäisajaksi on asetettu 45 päivää, joka perustuu toiveikkaaseen arvioon maailman käyttäytymisestä. Haluaisimme toimituksen siis puolessatoista kuukaudessa.

Kun ajamme simulaation, Companion ottaa jokaisella ajolla määritellyistä jakaumista sattumanvaraisen luvun ja sijoittaa sen yhtälöön, jossa meitä kiinnostava prosessin ulostulo syntyy. Kun suoritamme esimerkkisimulaation 50 000 kertaa, meille paljastuu, että kuvitteellinen prosessimme on kuin onkin kaukana hyväksyttävästä (kuva 4).

Simulaatio kertoo meille, että näillä tekijöillä 16,08 % kaikista tilauksistamme tulee myöhästymään annetusta 45 vuorokauden aikarajasta. Tästä voisimme jatkaa tekijöiden optimointiin, jossa voidaan kokeilla uusia tekijätasoja prosessin tekijöille. Mutta tässä tapauksessa käytämme herkkyysanalyysiä, jolla selvitämme miten vaihtelun vähentäminen parantaisi prosessia.

Graafista näemme vaihtelun vähentämisen vaikutukset spesifikaatiorajoissa pysymiselle, ja näemme että suurin vipuvaikutus saadaan aikaan toimitusten ja vastausaikojen hajonnan pienentämisellä. Valitsemme siis molempien tekijöiden puolittamisen ja simuloimme mallin taas uudestaan.

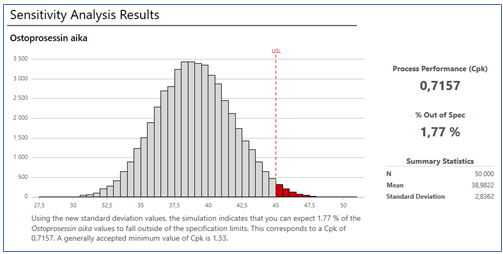
Nyt myöhästymisiä tulisi enää 1,77 %, vain koska puolitimme kahden tekijän hajonnan. Jotta saisimme prosessin kyvykkyyden hyvälle tasolle, täytyisi mallin tekijöitä vielä muuttaa. Tällaisessa alhaisen monimutkaisuuden mallissa on tietenkin selvää, että tekijöiden maksimiarvojen pienentämiset tulevat parantamaan suoraan lopputulosta. Mutta monimutkaisemmissa malleissa, joissa mallinnetaan monimutkaisia systeemejä ja joissa on mukana tekijöiden välisiä keskinäisriippuvuuksia tai epälineaarisuuksia, näiden tekijöiden ja ulostulon välisten suhteiden muutokset ole yhtä itsestään selviä.

Mihin Monte Carloa voidaan käyttää?

Monte Carlo on systeemien analysoinnin työkalu, jossa malliin liitettyjen tekijöiden epävarmuuden avulla voidaan simuloida tuotteen, prosessin tai tapahtuman todennäköistä lopputulosta. Simulaation etu reaalimaailmasta tehtäviin havaintoihin tulee juuri toistojen lähes rajattomasta määrästä. Monte Carlo-analyysi on loistava menetelmä, jonka avulla saamme kuvan prosessin todennäköisestä lopputulemasta tekijöihin liitettyjen riskien, eli epävarmuuksien avulla.

Artikkeli päivitetty 18.11.2022