Saat loistavan idean, joka näyttäisi ratkaisevan työ- tai vapaa-ajan ongelmasi. Kuinka toimit? Ideaa on testattava ja kokeiltava, toteutuuko idea ja saatko haluamasi tuloksen tai tuoton. Yksinkertaista, eikö totta! Muutat yhden asian ja toteat, mitä tapahtuu, One Factor at a Time, OFAT /1,6/.
Mutta kuinka ollakaan, työkaverisi tai ystäväsi ideoivat lukuisia muitakin mahdollisuuksia, tekijöitä, jotka voisivat vaikuttaa. Olisi toki hyvä testata ja kokeilla näitä kaikkia ideoita, mutta se olisi työlästä ja vaivalloista. Voisitko testata kaikkia ideoita samanaikaisesti? Mutta silloinhan et voi tietää, mitkä tekijät vaikuttavat, vai voisitko sittenkin saada tekijän selville yhdellä kokeella, Design of Experiments (DoE) tai Taguchi-metodi /2,3,6/.
Artikkelissa käsitellään yksimuuttuja- (OFAT) ja monimuuttujatestejä/kokeita (DoE) sekä niiden etuja, rajoitteita ja haittoja todellisella legoauto-esimerkillä. Tarkemmin eri koemenetelmistä 2013 kurssiesitteissä ”Lean & Six Sigma” ja ”Quality Tools”.
Yhden tekijän testit ja kokeet (OFAT)
Tarkastelin yhden tekijän muuttamista viime vuoden artikkelissa ”Onnistuuko tuottavuuden ja laadun parannus”/4/. Täydennän tässä artikkelissa yksimuuttujatestausta ”advance” testeihin, joilla voi testata yhä pienempiä muutoksia pienemmillä testitoistomäärillä (OFAT).
Jos tulos on ennen ja jälkeen muutoksen kuvan 1 mukainen, voit olla melko varma, että olet löytänyt oivallisen idean ja saanut aikaan suuren efektin/parannuksen. Muutos on merkittävä suhteessa keskiarvoon (62%), hajonta on pieni keskiarvoon nähden (COV n. 20 %) ja prosessi on stabiili.

Todellisuudessa suurien muutosten (ero, efekti) aikaansaaminen on harvinaista – harvinaisempaa kuin lotossa 7 oikein. Usein odotettavissa oleva muutos on pieni suhteessa keskiarvoon ja satunnaiseen vaihteluun. Vertaa vaikka omaa palkankorotustasi tai vaikka laihduttamista, sähkön säästöä tai auton polttoaineen kulutuksen pienenemistä ajotapamuutoksessa!
Kuinka pieni muutos voidaan havaita? Kerätään ennen ja jälkeen muutoksen riittävästi dataa (taulukko 1) ja lasketaan näistä datoista keskiarvo ja verrataan keskiarvoja keskenään. Keskiarvon hajonta on pienempi kuin yksittäisten mittausten hajonta. Tunnetaan ”Keskeisenä raja-arvolauseena” eli CLT/7/. Testausta nimitetään hypoteesitestaukseksi (kuva 2)/5,6/.
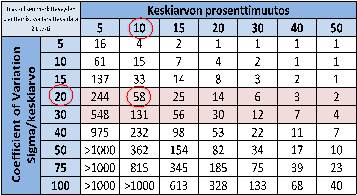

Kuinka toimit, jos dataa ei ole mahdollista saada riittävästi ja odotettavissa oleva muutos Δ on pieni suhteessa satunnaiseen vaihteluun σ eli pieni Δ/σ -suhde (= keskiarvon muutos % / COV %). Ainoa mahdollisuus on pienentää σ.
Tämä tilannehan on itse asiassa normaali. 5 – 10% muutos keskiarvoon 5-10 datalla olisi kohtuullista, mutta ei 58 + 58 (Δ/σ=0,5) 20%:n COV:lla (kuvan datan COV n. 20 %). Katso taulukko 1.
Kuinka datan määrää voidaan pienentää yhden tekijän kokeella (OFAT) eli kasvattaa Δ/σ-suhdetta?
Yksimuuttujakokeita/-testejä
Meillä on käytettävissä lukuisia erilaisia yksimuuttujatestejä/-kokeita/1,6/, joiden keskeisenä ideana on pienentää/suodattaa satunnaista vaihtelua σ eli kasvattaa Δ/σ -suhdetta. Tämä tapahtuu tunnistamalla taustamuuttujat (häiriöt) ja lohkomalla data ryhmiin. Tunnetuimpia menetelmiä ovat Parivertailu testit/suunnitelmat, Satunnaistetut täydelliset lohkosuunnitelmat (RCBD), Epätäydelliset lohkosuunnitelmat (BIBD), Latinalaiset neliösuunnitelmat (LSD), Graeco-Latinalainen neliösuunnitelmat (GLSD). Näitä kokeita kutsutaan 1-muuttuja DoE:ksi eli OFAT-kokeiksi
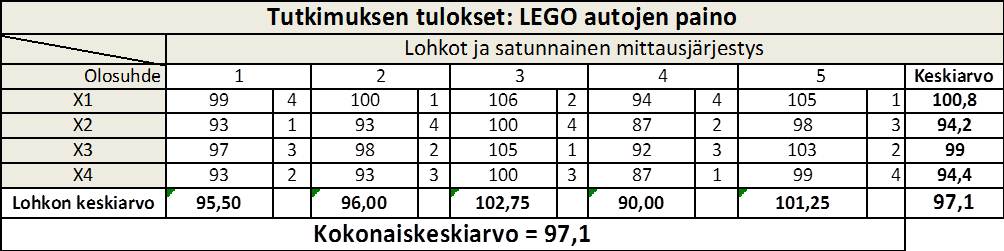
Yksimuuttujakokeita voi helposti demonstroida esim. legoautolla, jonka yhden komponentin X vaikutusta auton painoon testataan punnitsemalla neljällä tasolla (X1, X2, X3 ja X4) muiden komponenttien vaihtuessa satunnaisesti 1 ja 2 (A-F). Tekijän tasomäärän voi vapaasti valita 1-n. Tässä esimerkissä 4. Kaikkien komponenttien painot ovat eri suuruiset. Legoissa on sinitarraa. (Kuva 2, 3)


Luomalla 5 eri satunnaista olosuhdetta (lohko, block) palikoista ja punnitsemalla näistä komponenteista koottuja autoja satunnaisessa järjestyksessä, voidaan tutkittavan tekijän X1…X4 painot havaita (Taulukko 2). Esim. Lohko 1 on tässä: (A1, B2, C2, D1, E1, F2).
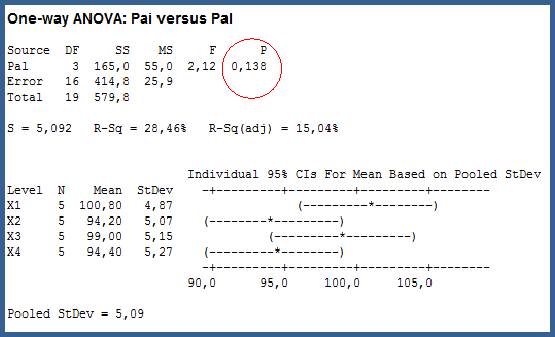
Tekijöitä X1-X4 analysoimalla ”perinteisesti” ei ole mahdollista erotella tilastollisesti komponentin X1…X4 vaikutusta auton painoon 20 mittauksella (5 mittausta/tekijä). Painojen keskiarvot poikkeavat liian vähän toisistaan suhteessa hajontoihin (taulukon oikea laita), jotta 95% varmuudella voisimme sanoa painovaikutusten poikkeavan toisistaan. 0-hypoteesia ei voi hylätä eli todeta yhden tai useamman X:n painovaikutuksen poikkeavan toisistaan, koska p>0,05 (0,138). Katso Minitab Anova -analyysi ja graafinen analyysi (Taulukko 3)/5/. Luottamusvälit (CI) menevät päällekkäin.
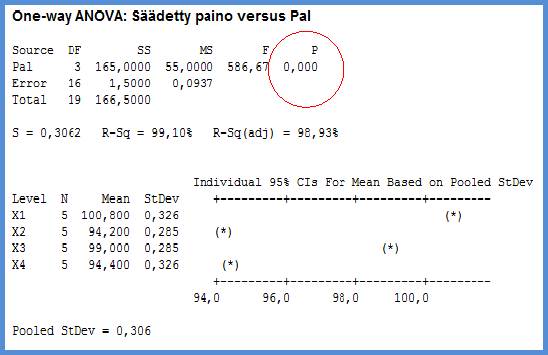
Tarkasteltaessa tarvittavaa datamäärää tehoanalyysillä/5/, voidaan havaita valtava muutos. Jos legoauton painoero kokeessa (difference) on 1,8 g, tarvittaisiin ei-lohkotussa tilanteessa 228 + 228 dataa (mittausta). Lohkotussa tapauksessa 3 +3 dataa (mittausta). Tällä olisi T&K, laboratorion tai tuotannon tuottavuuteenkin vaikutusta. On eri asia tehdä tuotannossa 500 testiä kuin 6 testiä! Taulukko 5.

Yksimuuttujakokeita voidaan edelleen tehostaa ”suodattamalla” taustamuuttujia pois latinalaisella neliösuunnitelmalla (Latin Square Design, LSD) tai Graeco-Latin Square Design (GLSD).
Kuvassa 4 ja 5 viisitasoiset yksimuuttujakoesuunnitelmat. Latin Square suunnitelmassa on kaksi hallittua taustamuuttujaa esim. työntekijät ja materiaalierät 5:llä tasolla ja tutkittavaa muuttujaa on merkitty kirjaimilla A-E. CLSD:ssä taustamuuttujia on 3 ja yksi tutkittava tekijä 5 tasolla.


Pienen tarkastelun jälkeen huomaa, että ”matriisithan” ovat japanilaisten tunnettuja SUDOKUJA/6/ ja samalla myös L25-ortogonaalimatriiseja (Taguchi-matriisi).
Mikä on yksimuuttujatestien ongelma? Saat yhä pienemmän ja pienemmän keskiarvomuutoksen esille. Jos oletetaan, että muutoksen toteutuskustannus, siis parannusinvestointi, pysyy vakiona, parannustulos tulee yhä kannattamattomaksi, mitä pienempiä muutoksia etsitään. Kuva 6

Yksimuuttujatekniikkaa ei käytetäkään huonon ”tehonsa”, luotettavuuden vuoksi Lean Six Sigmassa muussa tarkoituksessa kuin esitestauksessa PDSA-testeinä ja varmentamaan useiden samanaikaisten muutosten suurta efektiä, joihin se sopii erinomaisesti.
Yksimuuttujatestillä on kolme keskeistä heikkoutta:
- OFAT vaatii enemmän testejä DoE:n verrattuna (sama tarkkuus)
- OFAT:lla ei voi estimoida keskinäisvaikutuksia
- OFAT voi hukata optimiasetuksen
Seuraavaksi lyhyt esitys monimuuttuja kokeista Lego-autolla.
Monimuuttujatestit ja -kokeet (DoE, Taguchi)
Yksimuuttujakokeet (taulukot 1-4) voidaan ”helposti” laajentaa monimuuttujakokeeksi (taulukot 5-7) käyttämällä yksimuuttujakokeissakin käytettyä lohkomismenetelmää (Taulukko 6).

Lohkominen toteutetaan yleensä ns. ortogonaalimatsiisilla, jotka löytyvät lähes kaikista tilastosoftista ja kirjoista (/2,3/ Eero E. Karjalainen: Tuotteen ja prosessin optimointi Taguchi -menetelmällä 1989)
Monimuuttujakokeilla (DoE) on kaksi aivan ylivoimaista etua verrattuna OFAT -kokeisiin/testeihin – tarvittavien testien määrä pienenee merkittävästi ja keskinäisvaikutukset voidaan testata ja havaita. Lisäksi optimointi on paremmin hallittavissa.
Kuvassa 7 esimerkki legoautosta ja sen komponenttien testauksessa (esim. paino) tarvittavien testien määrä. Jos testaat 19 komponenttia yksimuuttujatestillä, tarvitset yli 524 288 testiä. DoE:lla testien määrä on minimissä 20. Katso taulukko 6 kohta 6 ”Screening -kokeet”.


Tehokkuuttakin tärkeämpi tekijä on keskinäisvaikutus, joka voidaan kokeissa huomioida. Jos olosuhde muuttuu, yksimuuttujakoetulokset ovat yleensä virheellisiä kun taas olosuhdemuutos (keskinäisvaikutus ja sen testaus) voidaan huomioida DoE -kokeissa ja analyysillä käyttämällä keskinäisvaikutuskuvaa.
Palataan legoautoesimerkkiin ja oletetaan, että taustamuuttujina toimineet komponentit A-F ovat ohjattavissa kuten myös X 2-tasolla. Jokaista vastin-komponenttia esim. pyörillä olevaa alustaa on kaksi kappaletta A1 ja A2. Kuva 8

Muodostetaan koesuunnitelma L8 -ortogonaalimatriisilla. Matriisi löytyy kirjoista tai esim. Minitab-softasta. Matriisi on 7-ulotteinen kohtisuora avaruus! Taulukossa 7 tekijät lohkottuna ja kokeen punnitut tulokset . Sama auto punnittu 2 kertaan esim. auto A1, B1, C1, D2, E2, F2, X1, Painaa 100 ja 101 g (1 g on punnitus/lukuvirhe)

Jokainen komponentti 2 x7 (A-X) =14 palikkaa on mitattu 16 mittauksella (punnituksella) 8 kertaan eli 112 mittaustulosta 16:lla mittauksella. Ei ihme, jos ortogonaalimatriisia kutsutaankin ”maagiseksi neliöksi”. Mitä enemmin tekijöitä, sitä tehokkaammaksi DoE tulee!
Minitabilla (tai käsin) on helppo laskea tuloksesta vastekuva, vaikutuskuva (huomaa: aina tulee Pareto) ja tehdä varianssianalyysi ja optimoida (esim. maksimoida) legoauton paino Minitabin Optimizerilla (kuvat 9-12).
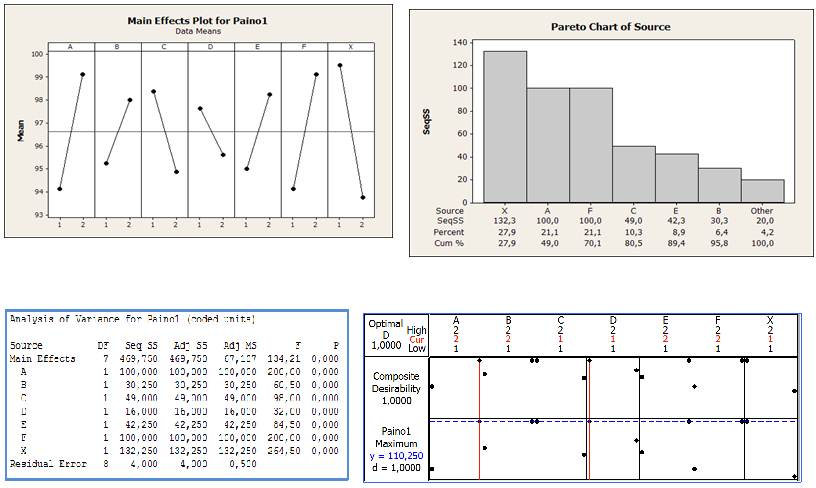
Jos legoautossa haetaan maksimipainoa, se saadaan yhdistelmästä A2, B2, C1, D1, E2, F2 ja X1. Maksimipaino on 110,25g. Huomaa, kuinka kaikkien komponenttien painoa käytetään hyväksi maksimipainon aikaansaamiseksi. Yhtä hyvin olisimme voineet hakea minimipainon tai jonkin haluamamme välipainon. Minitab Optimizer olisi asian hoitanut. Minitab olisi optimoinut samanaikaisesti painon lisäksi jopa 24 muuta ominaisuutta, mittaa. Yhteensä siis 25. Huikeaa tietotekniikan edistystä ja optimointia, jota ei olisi voinut 1990-luvulla edes kuvitella.
Jos maksimointi olisi tehty X1:llä (yksimuuttujana), olisi maksimi paino ollut keskiarvoltaan 98,5 g ja tulos olisi vaihdellut sattumalta 88,75 – 110,25 g:n välillä. Todella epävarmaa. Tästä syystä yksimuuttujatestejä ei pitäisi käyttää, jos ei taustamuuttujia voi vakioida tai kiinnittää. Yksimuuttujakokeen käyttö on hyvin kyseenalaista muussa kuin muutosten varmentamisessa. Yksimuuttujakoe ei ole ”tietellisesti” pätevä!
Yhteenveto
Yksimuuttujakokeen keskeisenä ongelmana on, että normaalilla menetelyllä ilman parivertailua tai muita lohkomistekniikoita, havaittavan muutoksen on oltava suuri suhteessa hajontaan tai vastaavasti näytemäärä suuri, jos Δ/σ –suhde on pieni. Tämä käytännössä estää jatkuvan parantamisen. Jos vielä muut tekijät voivat muuttua, vielä kyseenalaisemmaksi yksimuuttujakoe tulee.
Yrityksen tuottavuuskehitys pysähtyy ja/tai virheet/saanto/tapaturmat saavuttavat hajonnan määrittämän saturaatiotilan – ei kehitystä. Tämä tilanne havaitaan hyvin monissa palvelu- ja tuotanto-orgnisaatioissa, mutta tilannetta ei tunnisteta.
Meillä on laatuteorian mukaan kaksi tekniikkaa (stabiilisuus ja parannus), jolla voidaan kehitystä edistää. SPC:llä (esim. laatutaulu, kehittänyt E. Karjalainen 1981) voidaan ”ilman” kokeita (keinotekoista muutosta) havaita erityisyyt ja ryhtyä toimenpiteisiin tehokkaammin kuin ammattitaidolla ja SPC:n saavuttaessa saturaation (ei erityissyitä), on käytettävä DoE/Six Sigma -menetelmiä, joilla keinotekoisesti aiheutetaan muutos, erityissyy, joka mahdollistaa analysoinnin ja optimoinnin.
Ammattitaidolla saavutetaan normaalisti noin 2 sigman eli 65-75% hyväksymistaso ja maksimissaan 93, 4 %. SPC:llä hyväksymistaso nousee yleensä yli 95% ja DoE:lla NOLLA-virhe ei ole mahdoton. Six Sigman normitaso on pienempi kuin 3,4 ppmo eli Cp=2. Cp-indeksi japanilaisilla on 4,5 – 6! Opetus: vaihda menetelmää, tuottavuus- tai laatujärjestelmää, jos et saavuta riittävää edistystä! Analogia: Hanki silmälasit, jos näkösi on heikko tai tihrustat! Kuva 13.
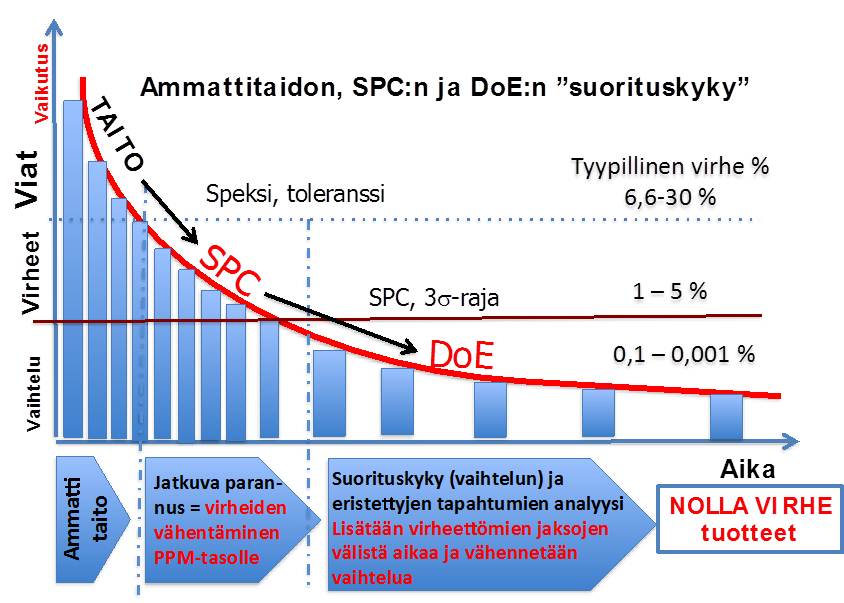
Kuvassa 14 todellinen käytännön esimerkki eri menetelmien teohosta samaan tuotteeseen.

Monimuuttujakokeet ovat tehokkaita ja luotettavavia. Pienellä koemäärällä voidaan luotettavasti havaita tekijämuutokset ja vaikutuksen summautuvuuden ansiosta tekijöiden testauksen/kokeen kokonaishyöty kasvaa sitä enemmän, mitä enemmän tekijöitä on samanaikaisesti testissä. Keskinäisvaikutukset voidaan havaita ja optimointi toteuttaa tehokkaasti. Nykyaikaiset tilastosoftat ovat tehneet koesuunnittelusta, analysoinnista ja optimoinnista todella helppoja ”joka miehen ja naisen työkaluja”.
Tästä johtuen Lean Six Sigmassa, jossa pyritään maksimaaliseen parannukseen minimikustannuksin, käytetään ensi sijassa monimuuttujakokeita parannusvaiheessa. Itse asiassa Six Sigma DMAIC -projektit ovat laajennettuja DoE-projekteja.
Monimuuttujatekniikassa tuottavuutta/kehitystä rajaavaksi tekijäksi tulee mittaus ja mittauksen virhe, johon on kiinnitettävä erityistä huomiota. Gage R&R ja muut menetelmät, jolla mittaus varmistetaan ja minimoidaan sen osuus kokonaisvaihtelusta, on tärkää. Tästä johtuen tiede ja myös yritykset (tuottavuus/saanto) edistyvät kehittämällä mittaustekniikkaa.
Lähteet:
1. Moen, Nolan, Provost: Quality Improvement Through Planned Experimentation, 2012
2. Eero E. Karjalainen: ”Tuotteen ja prosessin optimointi Taguchi- menetelmällä” 1989
3. Eero E. Karjalainen: ”Teollinen koesuunnittelu – Esimerkkejä Suomessa toteutetusta kokeellisesta tuotteen ja prosessin suunnittelusta Taguchi- menetelmällä” 1992
4. Eero E. Karjalainen: ”Onnistuuko tuottavuuden ja laadun parannus” 17.12.2012
5. Ryan, Joiner, Cryer: Minitab Handbook , sixth edition, 2012
6. Douglas C. Montgomery: Design and Analysis of Experiments, 2013
7. Douglas C. Montgomery: Introduction to Statistical Quality Control, 2013
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.


Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.