Johdanto
Monet nykyaikaisen tilastotieteen kehittymiseen vaikuttaneet tilastotieteilijät, kuten Sir Ronald A. Fisher ja George E. P. Box ovat myös kehittäneet monia koesuunnittelun menetelmiä. Sir R. A. Fisherin varhainen työ 1900–luvun alussa tilastollisen data-analyysin ja koesuunnittelun parissa mahdollisti tieteellisen menetelmän soveltamisen teollisiin ongelmiin (Box, 1989).
Koesuunnittelun avulla voidaan parantaa laatua sairaaloissa ja muissa palveluorganisaatioissa samoin, kuin tehtaissa. Kehittyneemmät koesuunnittelumenetelmät toimivat insinöörien ja tutkijoiden työkaluina, kun he pyrkivät suunnittelemaan tuotteita, jotka harvoin epäonnistuvat. Tämän kaltainen teoreettisen menetelmän sovellusalueen laajentuminen tieteellisestä menetelmästä käytännön työkaluksi vaikuttaa teolliseen tehokkuuteen ja parantaa elämän laatua (Box, 1989).
Historiaa
Koesuunnittelun historia voidaan jakaa neljään aikakauteen. Ensimmäistä aikakautta, maatalousaikakautta johti Sir. R. A. Fisherin (Kuva 1) uraauurtava työ 1920-luvulla ja 1930-luvun alussa koesuunnittelun menetelmien parissa. Tähän aikaan Fisher työskenteli Rothamstedin maatalouskoeasemalla Lontoon lähellä. Fisher havaitsi, että tapa, jolla kokeista kerättiin dataa usein haittasi datan analysointia. Samaan aikaan englantilainen tilastotieteilijä F. Yates (Kuva 2) kehitti myös koesuunnittelun menetelmiä. Fisherin yhteistyö monen eri alueen tutkijan kanssa johtivat Fisherin kehittämään kolme koesuunnittelun perusperiaatetta, nämä olivat: 1) satunnaistaminen (randomization) 2) toistaminen (replication) ja 3) lohkominen (blocking). (Montgomery, 2012; Peralta 2013)


Koesuunnittelun toinen aikakausi tai teollinen aikakausi alkoi 1930-luvulla ja sitä vauhditti G. E. P. Boxin (Kuva 3) ja K. B. Wilsonin (1951) kehittämä vastapintamenetelmä (response surface methodology = RSM). Box ja Wilson (1951) havaitsivat, että monet teolliset kokeet erosivat vastaavista maatalouden kokeista kahdella tavalla, 1) vastetta voidaan havainnoida lähes välittömästi ja 2) tutkija saa pienestä määrästä ajoja selville informaatiota, jota voidaan käyttää uusien kokeiden suunnittelemiseen. Teollisen aikakauden aikana myös erilaisten optimaalisten koesuunnitelmien käyttö yleistyi. (Montgomery, 2012)

Länsimaisen teollisuuden kasvava kiinnostus laadunparantamisesta alkoi 1970-luvun lopulla. Tämä oli alkuna kolmannelle koesuunnittelun aikakaudelle. Tutkijoilla, kuten G. Taguchi (Kuva 4), C. F. J. Wu ja R. N. Kackar oli suuri vaikutus lisääntyneeseen kiinnostukseen koesuunnittelun menetelmiä kohtaan. Tähän aikaan Taguchi esitteli koesuunnittelumenetelmänsä, niin sanotut robustit parametrisuunnitelmat. Taguchin työn myötä koesuunnittelun menetelmät levisivät monille eri teollisuuden aloille, kuten autoteollisuuteen, lentokoneteollisuuteen ja puolijohdeteollisuuteen. (Montgomery, 2012)


Koesuunnittelun neljännellä aikakaudella tutkijat ja soveltajat kiinnostuivat uudelleen erilaisista kokeensuunnittelun menetelmistä. Samoin erilaisten tietokoneohjelmien ominaisuudet kokeiden suunnitteluun sekä analysointiin lisääntyivät huomattavasti ja näiden menetelmien opettamisesta tuli osa yliopistojen opinto-ohjelmia. (Montgomery, 2012)
Joitakin teollisen koesuunnittelun menetelmiä
Seuraavassa on kaksi perinteistä koesuunnittelumenetelmää esitelty hieman tarkemmin. Nämä ovat full factorial -kokeet, joista esimerkkinä on käytetty kahden tekijän full factorial -koetta ja vastaavaa kahden tekijän vastepintakoetta. Esiteltyjen full factorial -kokeiden ja vastepintakokeiden analysointi on hyvin samankaltainen. Molemmissa tilanteissa sovitetaan lineaarista mallia käyttämällä pienimmän neliösumman menetelmää (ordinal least squares = OLS) sekä tutkitaan mallin termien merkitsevyyttä ja mallin sopivuutta, kunnes päädytään lopulliseen malliin.
Kaksitasoiset full factorial -kokeet (two lewel full factorials)
Koetta varten valitaan aluksi jokin määrä muuttujien tasoja kullekin muuttujalle. Tämän jälkeen suoritetaan koe kaikilla mahdollisilla kombinaatioilla. Kaksitasoiset full factorial -kokeet ovat tärkeitä, koska ne vaativat vähän ajoja ja niiden tulokset on helposti tulkittavissa. (Box, Hunter & Hunter , 2005)
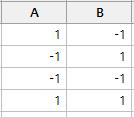
Kuvassa 6 on esitetty kaksitasoisen full factorial -kokeen suunnittelumatriisi. Kuvasta huomataan, että ”high” –tasoa vastaa suunnitelmassa 1 ja ”low” – tasoa -1. Vastaavasti huomataan suunnittelumatriisissa olevan kaikki A:n ja B:n yhdistelmien eri kombinaatiot.

Kuvassa 7 on graafinen esitys 2-tasoisen full factorial -kokeen suunnittelumatriisista. Kuvasta 7 huomataan, että suunnitelmaa voidaan kuvata neliöllä, jossa A:n ja B:n eri kombinaatiot muodostavat neliön kärkien koordinaatit. Koetta tehtäessä ajetaan koe kärkien eri kombinaatioilla ja mitataan aina vastaava vasteen arvo. Tämän jälkeen näin saatuun aineistoon sovitetaan lineaarista mallia. (Box, Hunter & Hunter 2005;Montgomery 2012)
Kaksitasoisessa full factorial -kokeessa sovitetaan dataan kaavan 1 mukaista mallia (Box, Hunter & Hunter 2005; Montgomery 2012)

Kaavasta 1 nähdään, että sovitettava malli on lineaarinen parametrien ja selittäjien suhteen. Malli on siis lineaarinen regressiomalli ja lineaarinen malli (Grönroos 2003). Kyseisessä regressiomallissa on päävaikutukset sekä tekijöiden yhdysvaikutukset ja virhetermi (ε). Mallia sovitettaessa mielenkiinto keskittyy parametrien(β), arvojen estimointiin ja sen analysointiin, onko mallin termi merkitsevä ja pitääkö sen olla mukana mallissa. Mallin termit, jotka eivät ole tilastollisesti merkitseviä voidaan poistaa mallista. Malli on kuitenkin hierarkinen, joten päävaikutuksen poistaminen ei ole mahdollista ennen kuin kaikki yhdysvaikutukset, jossa ne ovat mukana on poistettu.
Vastepintamenetelmä
G. E. P. Box ja K. B. Wilson esittelivät vastepintamenetelmän (response surface methodology =RSM) julkaisussaan vuonna 1951. Vastepintamenetelmän, samoin kuin kaikkien muidenkin kokeensuunnittelun menetelmien, tavoite on mallintaa tekijöiden ja vasteen välistä suhdetta ja löytää vasteelle esimerkiksi optimiarvo. Box ja Wilson (1951) ehdottavat tekijöiden ja vasteen välisen riippuvuuden kuvaajaksi toisen asteen polynomia, koska tällaisen polynomin approksimointi ja soveltaminen on helppoa, vaikka tutkittavasta prosessista tiedetään vähän. Montgomery (2012) kuitenkin toteaa, että tällainen toisen asteen polynomi, ei todennäköisesti ole hyvä approksimaatio tekijöiden ja vasteen väliselle suhteelle tekijöiden määrittämässä avaruudessa, mutta pienessä alueessa tällainen approksimaatio kuitenkin toimii suhteellisen hyvin.

Kuvassa 8 on esitetty kahden muuttujan kokeen suunnittelumatriisi. Kuvasta huomataan, että ”high” –tasoa vastaa suunnitelmassa 1 ja ”low” – tasoa -1. Samoin huomataan, että A:n ja B:n kombinaatioiden lisäksi suunnitelmassa on keskipisteitä (0,0) ja aksiaalipisteitä (axial point) (±1,414… , ± 1,414…) Vastaavasti huomataan suunnittelumatriisissa olevan kaikki A:n ja B:n yhdistelmien eri kombinaatiot eli neliön kärkipisteet.

Kuvassa 9 on graafinen esitys kahden muuttujan vastepintakokeen suunnittelumatriisista. Samoin kuvasta 9 uomataan, että suunnitelmaa voidaan kuvata neliöllä, jossa A:n ja B:n eri kombinaatiot muodostavat neliön kärkien koordinaatit. Erona aikaisempaan 2-tasoiseen full factorial -kokeeseen, ovat neliön keskelle tulleet keskipisteet ja kunkin sivun keskelle, neliön keskelle on tullut niin sanottu aksiaalipiste (axial point). Aksiaalipisteiden etäisyyttä neliön keskipisteestä merkitään α:lla. Aksiaalipisteen etäisyyden arvo (α:n suuruus) määräytyy suunnitelman ja sen mukaan halutaanko suunnitelman olevan ortogonaalinen vai kääntyvä. Koetta tehtäessä ajetaan koe kaikilla pisteiden eri arvoilla ja mitataan aina vastaava vasteen arvo. Tämän jälkeen näin saatuun aineistoon sovitetaan lineaarista mallia. (Box, Hunter & Hunter 2005;Montgomery 2012)
Kahden tekijän vastepintamenetelmässä sovitetaan dataan seuraavaa mallia, koska tekijöiden määrä esimerkissä on 3, kaavassa k=2. (Montgomery 2012)
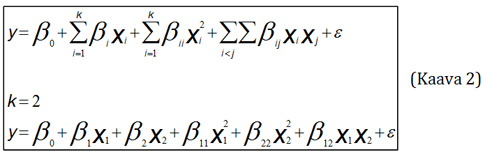
Malli (Kaava 2) on lineaarinen parametrien (β) suhteen, mutta ei selittäjien (x) suhteen. Malli on siis epälineaarinen regressiomalli ja lineaarinen malli (Grönroos 2003). Sovitettavassa mallissa on päävaikutukset sekä tekijöiden yhdysvaikutukset ja toisen asteen termit sekä virhetermi (ε). Mallia sovitettaessa mielenkiinto keskittyy parametrien (β), arvojen estimointiin ja sen analysointiin, onko termi merkitsevä ja pitääkö sen olla mukana mallissa. Mallin termit, jotka eivät ole tilastollisesti merkitseviä voidaan poistaa mallista. Myös tämä malli on hierarkinen, joten päävaikutuksen poistaminen ei ole mahdollista ennen kuin kaikki yhdysvaikutukset tai toisen asteen termit, jossa ne ovat mukana on poistettu.
Yhteenveto
Koesuunnittelun menetelmiä on olemassa useita, joita voidaan soveltaa eri tilanteissa. Tässä on esitelty vain muutama niistä. Edellä esitellyt koesuunnittelun menetelmät on valittu siten, että ne esittelevät kokeensuunnittelun keskeisiä periaatteita kuten full factorial kokeet tai niiden kehittyminen on omalta osaltaan ollut edesauttamassa teollisen koesuunnittelun menetelmien kehittymistä, esimerkiksi vastepintamenetelmä.
Hyvän mahdollisuuden erilaisiin teollisen kokeensuunnittelun menetelmiin tutustumiselle ja käytännön oppimiselle tarjoavat esimerkiksi erilaiset koesuunnittelu- tai Six Sigma-koulutukset. Kursseilla käydään opetetut menetelmät käytännön esimerkkien kautta läpi ja opetellaan myös tulosten analysointia, jotta huomataan menetelmien tehokkuus käytännön ongelmien ratkaisemisessa.
Lähteet:
- Box, G. E. P., 1989. Philosophical Transactions of the Royal Society of London. Series A, (), pp. 617-630.
- Box, G. E. P., Hunter, J. S. & Hunter. W. G., 2005. Statistics for Experimenters: Design, Innovation, and Discovery. John Wiley & Sons, Inc.
- Box, G. E. P & Wilson, K. B., 1951. On the Experimental Attainment of Optimum Conditions (with discussion). Journal of the Royal Statistical Society, Series B, 13(1), pp. 1-45.
- Grönroos, M., 2003. Johdatus tilastotieteeseen kuvailu mallit ja päättely. Oy Finn Lectura Ab.
- Montgomery, D. C., 2012. Design and Analysis of Experiments. John Wiley & Sons, Inc.
- Peralta, M., 2013. Design of Experiment. Createspace Independent Pub.
- Schmidt, S. R. & Launsby, R. G., 1994. Understanding Designed Experiments. Air Academy Press.
Internet lähteet:
- http://rsta.royalsocietypublishing.org/ (viitattu 4.3.2015)
- http://en.wikipedia.org/wiki/George_E._P._Box (viitattu 20.2.2015)
- http://en.wikipedia.org/wiki/Ronald_Fisher (viitattu 20.2.2015)
- http://en.wikipedia.org/wiki/C.F._Jeff_Wu (viitattu 20.2.2015)
- http://www.york.ac.uk/depts/maths/histstat/people/taguchi.gif (viitattu
- 20.2.2015)
- http://www.york.ac.uk/depts/maths/histstat/people/yates.gif (viitattu 20.2.2015)
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.

Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.